閑話休題その2 今度は少し高尚なお話。
理系の皆さんなら、聞いたことあるかもしれません。
1から100まで全部足すといくつになる?
1+2+3+4+5+6+7+8+9+10+11+12+13……???
1+100=101
2+99=101
3+98=101
‥‥‥
50+51=101
従って 101×50=5,050
ガウスが小学生の時、瞬時に答えた。これ有名な逸話です。
カール・フリードリヒ・ガウス(1777年~1855年)
ご存じドイツの数学者、天文学者、物理学者。
複素平面上での指数関数と三角関数の関係
| e | ネイピア数 | e=2.718281828459045‥ |
| π | 円周率 | π=3.141592653589793238‥ |
| i | 虚数 | i×i=-1 i=√-1 |
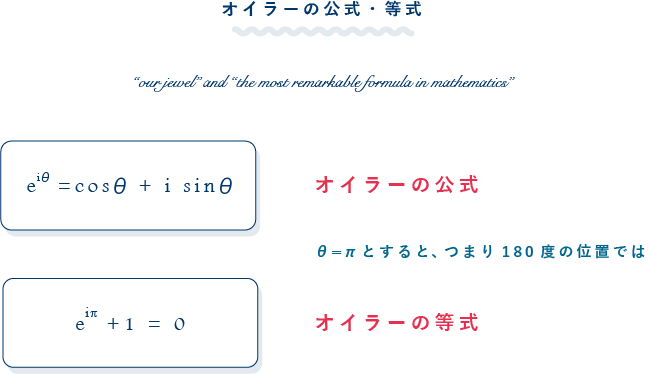
数学史上最も美しい等式、無理数と虚数が整数を生む。
レオンハルト・オイラー(1707年~1783年)
スイス生まれ、サンクトペテルブルクで活躍した数学者。
何でここでこんな話をするかといえば、特に開発者の皆さん
オイラーのような発想の転換を! 足し算を掛け算にする まさに発想の転換で、課題を簡単に解決する
見よ、オイラーの美しき等式を! APPLE製品のように、売れるものはシンプルで美しい
